早稲田大学 基幹理工学部
応用数理学科
Department of Applied Mathematics
School of Fundamental Science and Engineering, WASEDA University
News & Information [Archive]
あらわす、つなげる、うみだす
― 応用数理は未来への扉
AIやデータサイエンスが社会を変革する今、その根底にあるのは数学の力です。この時代に求められるのは、数学の知識だけでも、ITスキルだけでもなく、実社会の課題解決に数学を応用できる人材です。応用数理学科では、現象数理・統計数理・情報数理の三つの柱を通じて、抽象的な理論と現実の具体的な課題を結びつけられる人材を育成します。卒業生はIT企業、金融機関、メーカーの研究開発部門、教育研究機関、官公庁、コンサルティング会社など、幅広い分野で活躍しています。数学への深い理解と創造的な発想が出会う場所で、あなたの好奇心を未来につなげてみませんか。
あらわす驚き
自然現象や社会の動きや、ソフトウェアの中のデータ処理など、身のまわりにひそむ複雑な構造を、数学の力で「見える」かたちにする。その驚きと感動こそが、応用数理の醍醐味です。応用数理学科では、数学科と連携した基礎教育のもと、最先端の数理科学・統計科学・情報科学を深く学び、数学で世界を読み解く力を磨きます。
つなげる愉しみ
応用数理学科では数学と数学以外の分野をつなぐ融合研究が重要なテーマとなっています。情報学、統計学、工学、経済学、医学、生物学、化学、物理学など多様な分野への橋渡しを通じて、数学の力で科学技術や産業に貢献するとともに、数学の新たな可能性を拓く最先端の研究を行っています。
うみだす喜び
抽象的な理論が、現実世界を動かす革新的な技術に変わる瞬間。それは何にも代えがたい喜びです。応用数理学科では、気候変動の予測モデル、人工知能に関わる新しいアルゴリズム、金融リスクの評価手法など、数学を駆使して現実世界のさまざまな課題を解決する新技術を生み出しています。

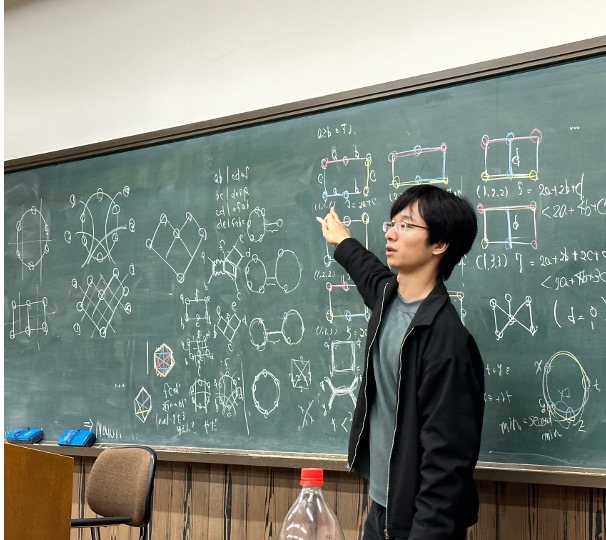
Curriculum
カリキュラム
応用数理学科の専門教育は、1年次の基幹理工学部の共通教育を終えた後に、2年次から始まります。数学科と連携した基礎数学の講義に加え、応用数理学科ならではのコンピュータ・情報、確率・統計、物理・化学の授業があり、さらに応用数理実験や演習・ゼミで応用力を鍛えます。4年次には研究室に配属され、最先端の応用数理の研究に挑戦します。4年次には大学院科目の先取り履修も可能です。幅広い分野の選択科目があり、自分の興味に合わせた学びができるのが特徴です。
確率・統計分野の専門科目の例
豊泉洋教授の「ビジネスと確率の数理」は、オペレーションズリサーチの一分野である「応用確率論」や「待ち行列理論」を使って、さまざまなビジネスモデルを確率的に分析・評価する方法を学ぶ講義です。複雑な現象やシステムのモデル化と解析に必要な確率論や確率過程の基礎をしっかり身につけたうえで、在庫管理、サービス産業、通信ネットワーク、コンピュータ、生産システムなど、実社会で使われている仕組みへの応用を考えていきます。講義だけではなく注文処理方式の違いによる店舗運営効率の良し悪しをシミュレーションする学生参加型の実験などもあり、ビジネスの背後にある数理の面白さを理論と実践の双方向から体感できる授業です。

List of Professors
教員一覧
応用数理学科では、現象・統計・情報の三分野を軸として、それぞれの専門分野の教員が最先端の研究と、世界トップクラスの教育を展開しています。これらの分野は互いに重なり合って、応用数理の豊かな世界を形成しています。
現象数理系
非線形系、ソリトン、数理物理、 応用幾何学、材料科学、系統解析,生命現象、自然現象、社会現象など、多様な現実の現象に対して数学的にアプローチします。
| 伊藤 公久 | 数理物質工学 |
| 大本 亨 | 特異点・トポロジー |
| 久藤 衡介 | 非線形偏微分方程式 |
| 高橋 大輔 | 離散力学系 |
| 平田 秋彦 | 数理物質工学・アモルファス構造 |
| 丸野 健一 | 数理物理・応用可積分系 |
統計数理系
数理統計学、確率論、時系列解析、金融・保険数理、医薬統計、データサイエンス、機械学習など、データに基づき意思決定を下すための数学的手法を研究・開発します。
| 清水 泰隆 | 数理統計・確率過程論 |
| 豊泉 洋 | 応用確率モデル・OR |
| 早水 桃子 | 離散数学・計算生物学 |
| 劉 言 | 数理統計・計算統計・時系列解析 |
情報数理系
情報理論、符号理論、暗号理論、 精度保証付き数値計算、最適化、グラフ理論、アルゴリズム論など、情報と計算に関わる諸分野に対する数学的アプローチを探求します。
| 荻田 武史 | 精度保証付き数値計算 |
| 柏木 雅英 | 精度保証付き数値計算 |
| 松嶋 敏泰 | 情報理論と応用 |
| 三枝崎 剛 | 符号理論・グラフ理論・暗号理論 |
| 村松 純 | 情報理論と応用 |
Career Paths after Graduation
卒業生・修了生の進路
主な就職先
クリックすると代表的な就職先の一覧が見られます。
学部卒業後の進路
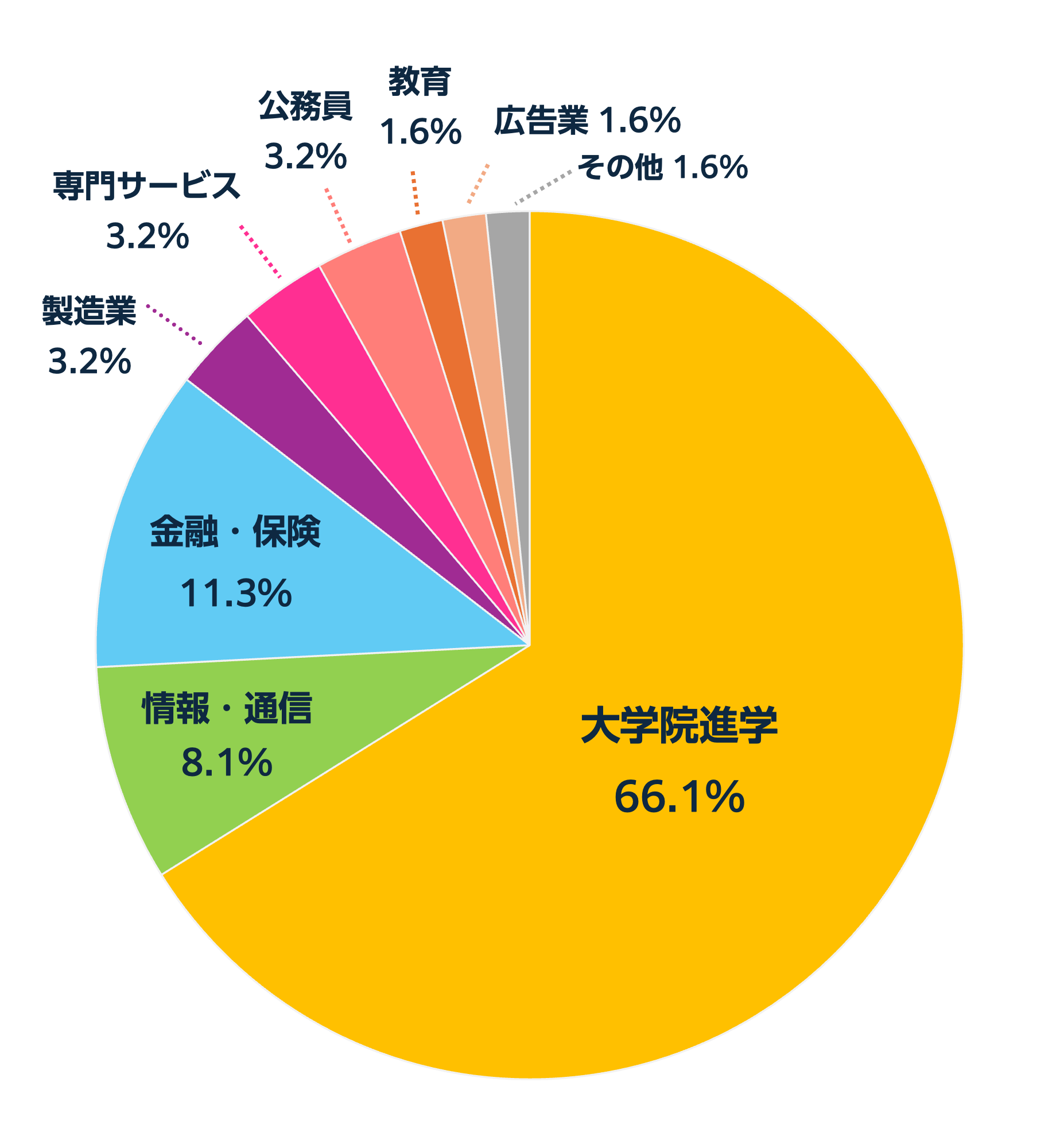
卒業後は応用数理の専門性を高めるために大学院修士課程に進学する学生が多いです。もちろん、応用数理学科は就職に強いのでIT企業や金融や商社やシンクタンクなどで活躍する卒業生たちも多数います。学部からの推薦枠をはじめとする就職サポート体制も充実しています。
修士課程修了後の進路
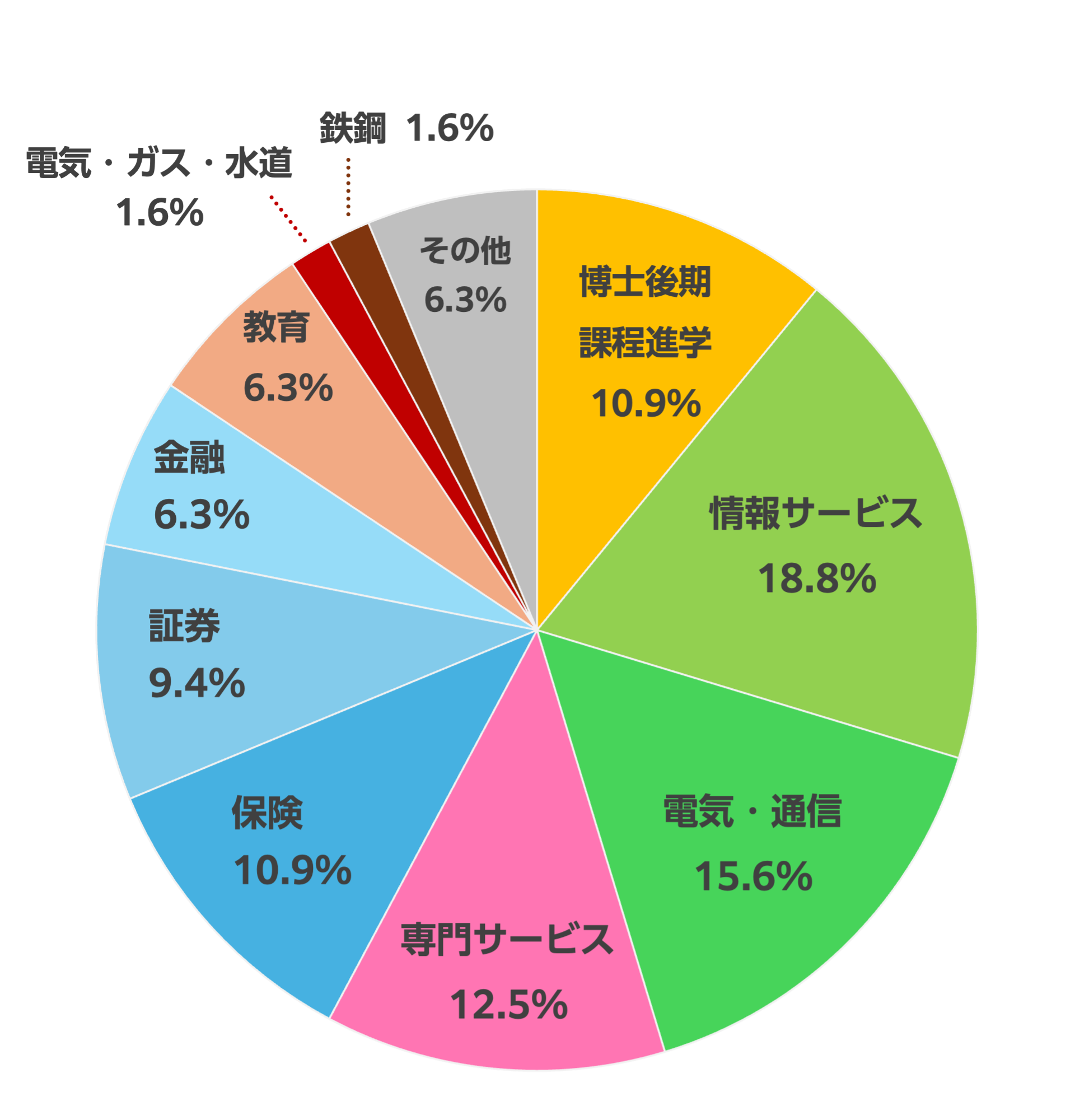
修士課程(数学応用数理専攻)修了後は、数理・情報・統計の強みを活かした多彩な進路があります。例えば、データサイエンティスト、システムエンジニア、ソフトウェア開発者、ITコンサルタント、クオンツ、アクチュアリーなどです。博士課程に進学して数理科学の専門性をさらに高めることもできます。

